In this blog post we discuss a MyCaffe implementation design of the paper “LoRA: Low-Rank Adaptation of Large Language Models” by Hu et al. [1] and describe how LoRA helps leverage the knowledge of the trained LLM to solve new specific problems in an efficient manner through fine-tuning. LLMs are immensely powerful but are created at significant compute cost and require substantial amounts of parameters to store the knowledge they learn. Often it is desirable to use the vast knowledge of these powerful LLM’s to solve new problems that involve new and often proprietary knowledge. Several methods used to focus an LLM to solve such new problems include retraining the entire model (very expensive and slow), using Retrieval Augmented Generation (RAG) that focuses on the existing knowledge of the model, or using a fine-tuning mechanism such as Low-Rank Adaption (LoRA) to add new knowledge to the model but do so in a way that leaves the original model unaltered.

LoRA is used to freeze the pre-trained model weights and inject trainable rank decomposition matrices into each layer of the Transformer architecture. This technique is used to adapt a pre-trained language model to a specific downstream task using a task-specific dataset and is useful when the task-specific dataset is small, and the pre-trained model is large. [2]
RAG, on the other hand, is used to combine a retrieval model with a language model. The retrieval model is an information retrieval system that retrieves relevant information from a large knowledge base. The language model is then used to generate a response based on the retrieved information. RAG is useful when the knowledge base is large, and the task requires the model to retrieve relevant information from it. [3] [4]
In summary, both LoRA and RAG share the goal of boosting pre-trained language models on specific tasks, but they take distinct approaches. LoRA focuses on efficient adaptation, introducing minimal changes to the model’s weights through low-rank updates. This makes it ideal for situations with limited task data and large, expensive LLMs. RAG, on the other hand, leverages the power of document retrieval. It integrates an LLM with a dedicated retrieval model that scours vast knowledge bases for relevant information. This makes RAG shine when tasks involve factual accuracy and require access to rich, external knowledge. Ultimately, the “better” technique depends on the specific requirements of your task. LoRA excels when efficiency and minimal data are paramount, while RAG thrives when comprehensive knowledge retrieval and factual grounding are key. Choose your tool wisely, considering the task at hand and the resources available, to unlock the full potential of your pre-trained language model.
LLM, Transformer and Attention Impact
Language models such as Chat-GPT, GPT and Encoder/Decoder models use transformer-based architectures. Internally, these transformer-based architectures, use many layers that each leverage an attention mechanism involving a Q, K, V calculations as discussed in the “Attention Is All You Need” paper by Vaswani et al. [5]. Within each of these attention-based layers, three important Linear layers are used to make these calculations and subsequently store a large amount of the LLM knowledge. Hu et al. [1] found that fine-tuning only the W_Q and W_V Linear layers with LoRA had nearly the same accuracy as fine-tuning all four Linear layers within the attention-based layer, resulting in a dramatic parameter and compute reduction for the fine-tuning process.

According to Hu et al. [1], using this technique reduced the number of trainable parameters for the 175B parameter GPT-3 model by 10,000x and reduced the GPU memory requirement by 3x. “LoRA performs on-par or better than fine-tuning in model quality on RoBERTa, DeBERTa, GPT-2 and GPT-3, despite having fewer trainable parameters, a higher training throughput, and, unlike adapters, no additional inference latency.” [1]
The designs discussed in this post are based on the ‘official LoRA’ implementation by Microsoft [6], where the LoRA algorithm applies new LoRA weights to the input data and the result is added to the existing layer’s output. A post from Lightning.AI indicates that their implementation is similar to Microsoft’s. [7]
A slightly different approach is introduced in ‘minLoRA’ by Jonathan Chang [8], where the LoRA algorithm adapts specific layer weights by adding the new LoRA weights to the existing weights themselves before they are used.
Inner Product (Linear) Layer
The MyCaffe InnerProduct, or Linear layer is a fundamental layer used throughout many models and is used extensively in transformer-based models. Each InnerProduct layer contains a set of learnable parameters, one for the weights and a second, optional set for the bias.
During the forward pass, the weights and (optionally) bias are applied to the input data to produce the output data.
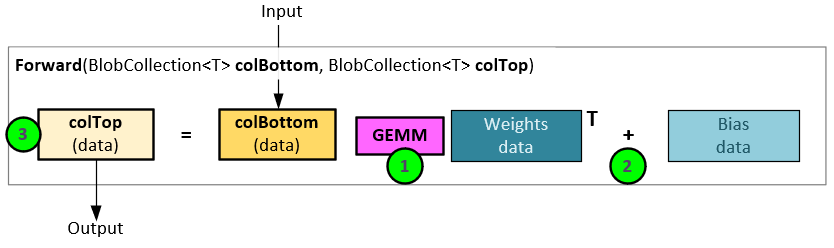
In an InnerProduct layer forward pass there are three steps to the calculation.
- A GEMM operation is performed between the input data (colBottom) and the internal Weight data.
- The results from step #1 are then added to the Bias data…
- … to produce the output data (colTop).
Similarly, during the backward pass, the weight and bias gradients are calculated from the input gradients.
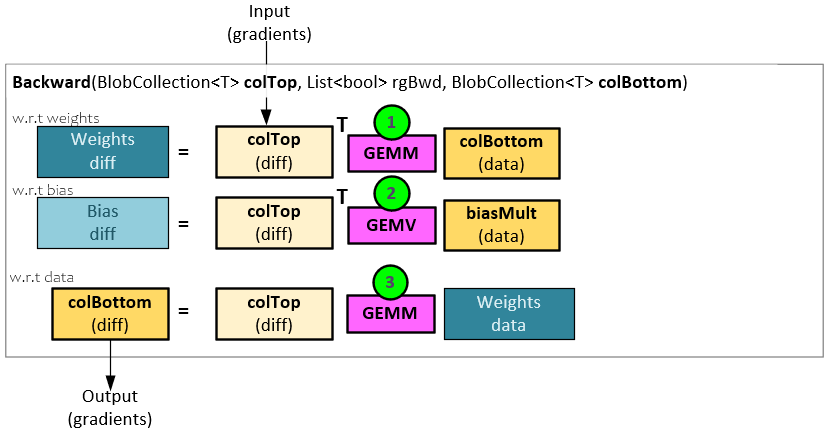
In the InnerProduct layer backward pass, the weight and bias gradients are updated along with the output gradients in the following steps.
- The weight gradients are updated by performing a GEMM operation between the input gradients and the previous input data (colBottom).
- The bias gradients are updated by performing a GEMV operation between the input gradients and an interna bias multiplier set to all 1’s.
- The output gradients are calculated by performing a GEMM operation between the input gradients and the weight data.
Adding LoRA to the InnerProduct (Linear) Layer
Introducing LoRA to the InnerProduct layer allows for adapting the effective weights while leaving the original weights unaltered (e.g., frozen).

Two hyper parameters impact how the LoRA weights alter the effective weights. The alpha setting regulates how much of the learning from the LoRA weights are applied to the effective weights. And the rank impacts how the initial weights are initialized. Note, the different implementations [6], [7], and [8] use these parameters slightly differently. Implementations from Microsoft [6] and Chang [8] use the rank and alpha to create a scaling factor (scaling = alpha/rank) where the scaling factor regulates how much of the LoRA weights are applied. Whereas the Lightning.AI implementation [7] uses the rank to scale the initialization of the LoRA_a weights and the alpha to scale how much of the LoRA weights to apply.
InnerProduct Layer Forward Pass with LoRA
During the forward pass, the original LoRA implementation [6] runs the InnerProduct layer forward pass untouched and then adds in the LoRA outputs to the results.

The following steps occur within the InnerProduct layer forward pass with LoRA, where the first three steps are the same as the standard InnerProduct layer forward pass.
- A GEMM operation is performed between the input data (colBottom) and the internal Weight data.
- The results from step #1 are then added to the Bias data…
- … to produce the x data.
- The input data (colBottom) is then passed to the LoRA Parameter for processing.
- The LoRA Parameter results are added to the previous x data to produce the final output data (colTop).
Within the LoRA Parameter, the LoRA weights are applied to the input data during the forward pass to create the effective weights applied to the input data which is where the learned weights from the fine-tuning are used.

During the forward pass, the LoRA Parameter takes the following steps to apply the fine-tuned weights to the input data.
- The outputs from the InnerProduct layer are passed to the LoRA Parameter.
- Optionally, the input data (x) is run through a Dropout layer to produce x1.
- A MATMUL operation is run on the x1 data and LoRA_a weights to produce the xA
- A second MATMUL operation is run on the xA data and the LoRA_b weights to produce the xAB data.
- The xAB data is then scaled using the scaling method (e.g., scaling by just Alpha [7], or scaling by Alpha/Rank [6] [8]) to produce the Scaled_xAB data.
- The Scaled_xAB data is then added to the original input from step #1 to produce the final output (colTop).
InnerProduct Layer Backward Pass With LoRA
During the backward pass with LoRA, the input gradients are applied to the LoRA weights which is where the fine-tuning learning occurs.
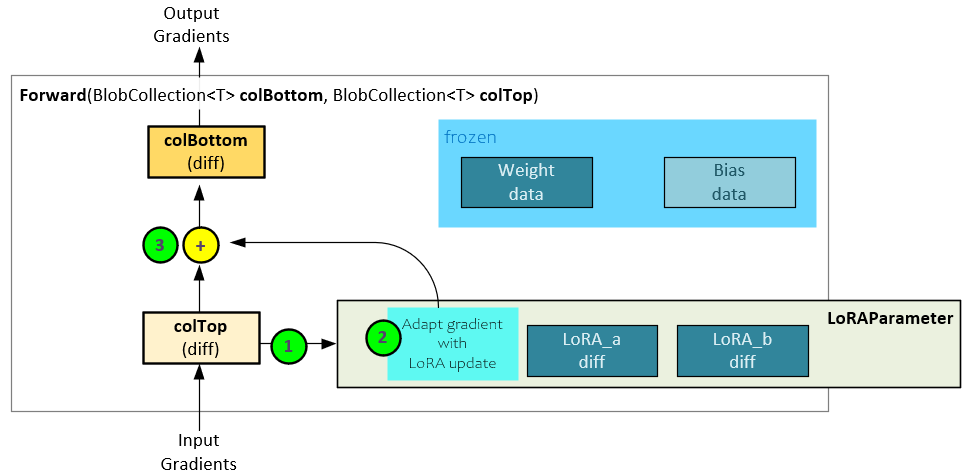
The following steps occur during the backward pass with LoRA.
- The input gradients (colTop diff) are passed to the LoRA Parameter for processing.
- The LoRA Parameter applies the input gradients to both the LoRA_a and LoRA_b weights to create their gradients and returns the updated output gradients.
- The original input gradients are added to the LoRA Parameter output gradients to produce the final output gradients (colBottom diff).
Within the LoRA Parameter, the backward pass updates the LoRA_a and LoRA_b gradients and produces the LoRA output gradients.
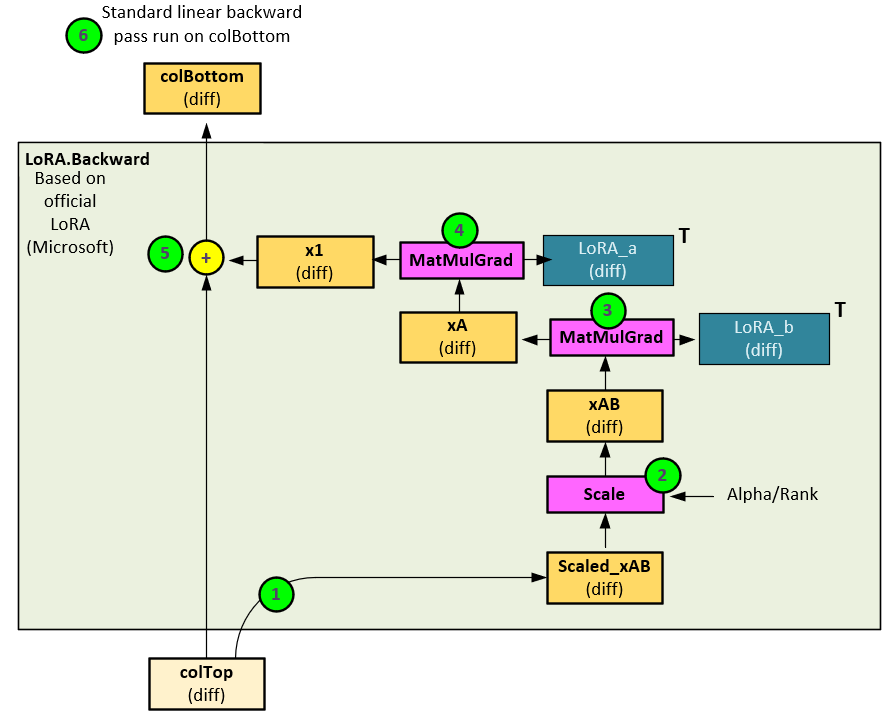
The following steps occur within the LoRA Parameter during the backward pass.
- The input gradients (colTop diff) are passed to the Scaled_xAB diff.
- The Scaled_xAB diff is then scaled using the scaling method (e.g., scaling by just Alpha [7], or scaling by Alpha/Rank [6] [8]) to produce the xAB diff gradients.
- The xAB diff is run backwards through the MatMulGrad function which calculates the gradients for both the xA diff and LoRA_b diff gradients.
- A second MatmulGrad function is run on the xA diff to calculate the gradients for both the x1 diff and LoRA_a diff gradients.
- The x1 diff gradients are added to the original input gradients (colTop diff) to produce the output gradients (colBottom diff) thus allowing LoRA weights to learn without impacting the original Linear layer weights.
All LoRA gradients (e.g., LoRA_a diff and LoRA_b diff) are applied to the weight data using the optimizer of choice such as Adam, AdamW or SGD.
Summary
In this post we discussed what LoRA is and how it dramatically reduces the parameter and compute requirements for fine-tuning any model using Linear layers, and in particular the Q and V Linear layers used within a Transformer based model such as Chat-GTP or GPT. In addition, we showed the specific steps of both the forward and backward pass demonstrating how LoRA fine-tunes a model without altering the original weights of the model.
Try LoRA for yourself with our LoRA Jupyter notebook that demonstrates a PyTorch based LinearLoRA layer solving a very simple learning example.
Happy deep learning with LoRA!
[1] LoRA: Low-Rank Adaptation of Large Language Models, by Edward J. Hu, Yelong Shen, Phillip Wallis, Zeyuan Allen-Zhu, Yuanzhi Li, Shean Wang, Lu Wang, and Weizhu Chen, 2023, arXiv:2106.09685
[2] Customizing Large Language Models: Fine-Tuning and Retrieval Augmented Generation, by Nischal Suresh, 2023, Medium
[3] Knowledge Graphs & LLMs: Fine-Tuning vs. Retrieval-Augmented Generation, by Tomaz Bratanic, 2023, neo4j
[4] Enhancing LLM Intelligence with ARM-RAG: Auxiliary Rationale Memory for Retrieval Augmented Generation, by Eric Melz, 2023, arXiv:2311.04177
[5] Attention Is All You Need, by Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin, 2017, arXiv:1706.03762
[6] GitHub:microsoft/LoRA, by Microsoft Corporation, 2023, GitHub
[7] Code LoRA From Scratch, by Lightning.AI, 2023, GitHub
[8] GitHub:cccntu/minLoRA, by Jonathan Chang, 2023, GitHub

